МОДЕЛЬ СИНТАКСИСА В СИСТЕМЕ МОРФОСИНТАКСИЧЕСКОГО АНАЛИЗА «TREETON»

SYNTACTIC MODELING IN THE «TREETON» MORPHOSYNTACTIC ANALYSIS SYSTEM

М.Г. Мальковский (malk@cs.msu.su)

А.С. Старостин (Anatoli.Starostin@avicomp.ru)

Московский Государственный Университет им. М .В .Ломоносова, Кафедра алгоритмических языков

В докладе предлагается формальная модель описания синтаксиса, сочетающая в себе формализмы зависимостей и составляющих (в духе А.В.Гладкого). Описывается система Treeton, предназначенная для морфосинтаксического анализа русского текста. Указанная синтаксическая модель интегрирована в систему Treeton. Излагается алгоритм синтаксического анализа, используемый системой. Приводится описание аппарата лингвистически содержательных штрафных функций, применяемого для уменьшения перебора в ходе анализа.

Система Treeton – это исследовательская компьютерная среда для работы с текстами, написанными на естественном языке. Она разрабатывается авторами на кафедре алгоритмических языков факультета ВМиК МГУ начиная с декабря 2004 года. Система была задумана как среда, с помощью которой было бы удобно проводить исследования, связанные с морфологией и синтаксисом естественных языков (прежде всего русского). На данный момент в системе уже функционирует модуль русского морфологического анализа. Этот модуль был создан на основе русского морфологического анализатора системы Starling (http://starling.rinet.ru) с использованием результатов, приведенных в [Мальковский 1985]. В связи с этим основные усилия авторов направлены на исследования в области синтаксиса.

Подход к синтаксическому анализу, принятый авторами, был изложен Н.В. Перцовым и С.А. Старостиным на международном семинаре Диалог’99 [Перцов, Старостин 1999] в докладе «О синтаксическом процессоре, работающем на ограниченном объеме лингвистических средств». В нем формулировалась концепция синтаксического анализатора, который опирается в основном на морфологические характеристики слов без использования богатой словарной информации о сочетаемости. Набор синтаксических отношений также сознательно сужался. Такая установка была продиктована в первую очередь тем, что в открытом доступе не существовало (и до сих пор не существует) формализованных словарей сочетаемости единиц достаточно большого объема. Очевидно, что такой анализатор не может во всех случаях строить структуры, полностью соответствующие требованиям современных синтаксических теорий. Такой анализ следует трактовать скорее как предварительную синтаксическую разметку, а не как полноценный синтаксический анализ. Результаты этой разметки (особенно при достаточно высокой точности) могут иметь практическое использование. Например, набор размеченных таким образом текстов толковых словарей может стать материалом для исследований в области семантики.

Данная статья посвящена опыту создания синтаксического анализатора в рамках упомянутой концепции. Основное внимание уделяется работающим в системе Treeton механизмам анализа, а не конкретному лингвистическому наполнению, работа над которым пока еще не завершена. Несмотря на это, авторы полагают, что приводимый материал может представлять интерес как для программистов, работающих с естественным языком, так и для лингвистов, в той или иной степени ориентированных на моделирование языковых процессов.

По аналогии с многими современными системами (в качестве примера можно привести среду GATE [Cunningham a.o. 2002]) в системе Treeton в качестве базовых используются такие понятия, как аннотация и множество аннотаций. Аннотация – это набор пар вида <атрибут,значение>, привязанный к некоторому отрезку текста. В системах такого рода обычно считается, что при работе с текстом каждый модуль получает на вход некоторое множество аннотаций, как-то преобразует его и передает следующему модулю. В качестве примера можно привести модуль морфологического анализа в системе Treeton. Этот модуль работает с множеством токенов (англ. token) – линейным списком отдельных аннотаций-токенов, каждая из которых соответствует определенному атомарному элементу текста (знаку пунктуации, непрерывной последовательности букв, набору цифр и т.п.). Модуль морфологического анализа выделяет из множества токенов последовательности, которые потенциально могли бы быть словоформами некоторой лексемы, анализирует эти последовательности и создает на их месте аннотации, соответствующие вариантам анализа. Полученное множество аннотаций подается на вход модулю синтаксического анализа. На рисунке 1 приводится пример множества аннотаций, состоящего из токенов и морфологических аннотаций, соответствующих входной строке «светло-зеленые».

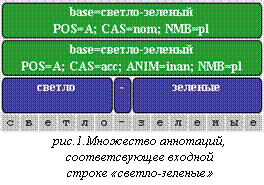Однако, для описания и реализации модуля синтаксического анализа аппарата аннотаций оказывается недостаточно. В частности, описывать связи между аннотациями можно лишь косвенно, вводя специальные атрибуты, значениями которых становятся идентификаторы других аннотаций. Это, в свою очередь, приводит к немотивированному усложнению алгоритмов и формализмов, работающих с аннотациями. Для решения этой и некоторых других проблем нами был разработан и интегрирован в систему Treeton аппарат тринотаций (рабочий термин, родившийся из соединения англ. "tree" и "annotation"). Понятие тринотации является, на наш взгляд, разумным расширением понятия аннотации. В разделе 1 мы приводим краткое описание этого аппарата. В разделах 2-4 приводится описание синтаксической модели, принятой в системе Treeton, которое опирается на понятия, введенные в разделе 1.

1. Тринотации и множества тринотаций

Тринотация – это аннотация, снабженная внутренней структурой – лесом с именованными связями, в узлах которого стоят другие тринотации.

Очевидно, что любая аннотация является также и тринотацией (с тривиальной внутренней структурой).

Тринотации удовлетворяют следующим аксиомам:

1) Если некоторая тринотация A является узлом внутренней структуры тринотации B, то отрезок текста, соответствующий A, всегда вложен в отрезок, соответствующий B, или совпадает с ним.

2) Граф развертки тринотации является деревом.

Граф развертки определяется следующим образом:

a) Если тринотация t не имеет внутренней структуры, то граф ее развертки определяется как <{t};⌀>.

b) 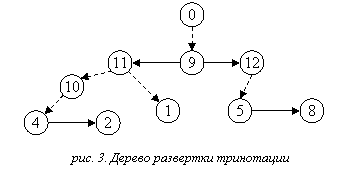Если внутренняя структура тринотации t представляет из себя набор направленных деревьев T₁,T₂...T_n, то граф G развертки этой тринотации может быть получен при помощи следующей процедуры: сначала в граф G добавляется узел t и все узлы и дуги деревьев T_i (i: 1,2,…,n), затем в граф G добавляется по одной служебной дуге для каждого дерева T_i, соединяющей t с корнем дерева T_i, после чего в граф G добавляются графы развертки всех узлов деревьев T_i.

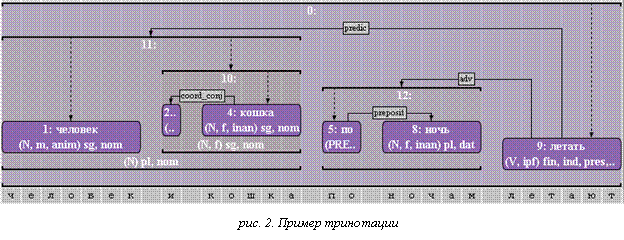На рисунке 2 приводится пример тринотации, а на рисунке 3 иллюстрируется свойство 2 для этой тринотации (пунктиром обозначены служебные связи).

В силу условия 2 далее всюду в тексте будем называть граф развертки деревом развертки тринотации. Легко видеть, что сформулированный набор условий не требует от тривиальных узлов дерева развертки тринотации попарного непересечения. Под тривиальными узлами подразумеваются тринотации, не имеющие внутренней структуры. Мы сознательно не стали накладывать это ограничение на тринотации, хотя для представления синтаксических структур оно кажется разумным. Дело в том, что при описании синтагматических отношений между единицами текста такое условие действительно всегда выполняется, но, как оказалось, множество тринотаций удобно использовать и для других целей, например, для хранения парадигматических классов тех или иных единиц. В этом случае приходится иметь дело, наоборот, с полным наложением дочерних элементов одной структуры.

Приведенное определение тринотации (с наложенным ограничением на пересечение тривиальных узлов дерева развертки) оказывается очень близким к определению размеченной системы синтаксических групп (РССГ) [Гладкий 1985: 56]. Тринотации и РССГ отличаются следующим: во-первых, на РССГ изначально наложено больше ограничений [Гладкий 1985: 50](аксиомa 3 из 1-ой группы, аксиомы 4,5 из 2-ой группы). Условия, схожие с указанными аксиомами, были использованы нами для конструирования штрафных функций (см. далее). Во-вторых, РССГ является по определению множеством непустых подмножеств П (в нашем случае за П следует принять множество тривиальных узлов дерева развертки тринотации). Следовательно, двух групп, включающих одинаковый набор элементов П, не может существовать. Тринотаций, содержащих одинаковый набор тривиальных тринотаций, может, напротив, быть сколько угодно (они могут вкладываться друг в друга "как матрешки").

Система Treeton предоставляет программный интерфейс, с помощью которого программист может без особого труда манипулировать тринотациями. Среди различных функций этого интерфейса важное место занимают элементарные преобразования тринотаций. Они понадобятся нам при описании языка синтаксических правил. Перечислим эти преобразования и приведем их краткое описание в терминах деревьев разверток.

Следует сказать, что служебные связи в дереве развертки бывают двух типов – сильные и слабые. Первые мы будем называть s-связями, а вторые w-связями. Слабые связи могут разрываться в ходе элементарных преобразований, а сильные нет. Подчеркнем, что обычные (не служебные) связи, так же как и s-связи, не могут разрываться. Условимся, что все описываемые ниже преобразования производятся над тринотацией t с деревом развертки T. Считается, что во всех случаях, когда тринотация, участвующая в преобразовании, берется извне (т.е. еще не принадлежит T), она имеет тривиальную внутреннюю структуру.

Преобразование link (h, s, r)

Это преобразование добавляет к внутренней структуре t неслужебную связь r, идущую от тринотации h к тринотации s. Отметим сразу, что это преобразование невозможно, если h или s совпадают c t или друг с другом. Следует также оговорить некоторые нюансы преобразования, связанные с аксиомой 2. Возможны 4 случая:

1. h ∉ T и s ∉ T

В этом случае, чтобы T осталось деревом, дополнительно проводится w-связь от t к h.

2. h ∉ T и s ∈ T

В этом случае преобразование возможно только тогда, когда в s входит w-связь. Обозначим хозяина этой связи как s_p. Если условие выполняется, то связь разрывается, после чего проводится w-связь от s_p к h.

3. h ∈ T и s ∈ T

В этом случае преобразование возможно только тогда, когда, во-первых, в s входит w-связь и, во-вторых, между s и h не существует направленного пути. При выполнении этих условий w-связь разрывается.

4. h ∈ T и s ∉ T

В этом случае не требуется разрывать связи или проводить дополнительные. Проверять ограничения также нет необходимости.

Преобразование addMemberWeak (b, m)

Это преобразование добавляет к внутренней структуре t w-связь, идущую от тринотации b к тринотации m. Отметим сразу, что это преобразование невозможно, если b и m совпадают друг с другом или если m совпадает с t. Необходимо также, чтобы b ∈ T и от b к m не было проведено w-связи. Возможны 2 случая:

1. m ∈ T

В этом случае преобразование возможно только тогда, когда, во-первых, в m входит w-связь и, во-вторых, между m и b не существует направленного пути. При выполнении этих условий w-связь разрывается.

2. m ∉ T

В этом случае не требуется разрывать связи или проверять ограничения.

Преобразование addMemberStrong (b, m)

Это преобразование аналогично преобразованию 2 с той лишь разницей, что проводится не w-, а s-связь. Кроме того, перед преобразованием от b к m уже может быть проведена w-связь. В этом случае она просто заменяется на s-связь.

Преобразование aggregateWeak (m)

В ходе этого преобразования создается новая тринотация b, от которой проводится w-связь к тринотации m. Очевидно, что m не может совпадать с t. Возможны 2 случая:

1. m ∈ T

В этом случае преобразование возможно только тогда, когда в m входит w-связь. Обозначим хозяина этой связи как m_p. Если условие выполняется, то связь разрывается, после чего проводится w-связь от m_p к b.

2. m ∉ T

В этом случае проводится w-связь от t к b.

Преобразование aggregateStrong (m)

Это преобразование аналогично преобразованию 4 с той лишь разницей, что от тринотации b к тринотации m проводится не w-, а s-связь.

Следует отметить, что в системе Treeton все вышеописанные преобразования могут производится в двух режимах: в режиме контроля за попарным непересечением тривиальных тринотаций и в свободном режиме (без такого контроля). Кроме того, система осуществляет контроль за выполнением аксиомы 1 в ходе элементарных преобразований. Объемлющие тринотации автоматически меняют свои размеры при изменении размеров своих потомков.

Кроме программного интерфейса в системе Treeton на данный момент функционируют два формальных аппарата для работы с тринотациями:

1. Язык Scape для работы с тринотациями как с аннотациями, не позволяющий манипулировать внутренними структурами тринотаций. Этот язык является свое рода наследником языка Jape+ [Shafirin a.o. 2004].

2. Анализатор Treevial, включающий в себя специальный декларативный язык, на котором могут записываться правила синтаксического анализа, и модуль автоматического анализа текста на естественном языке по этим правилам. Обзор этого формального аппарата на примере русского языка приводится в следующих разделах.

2. Синтаксический анализатор Treevial

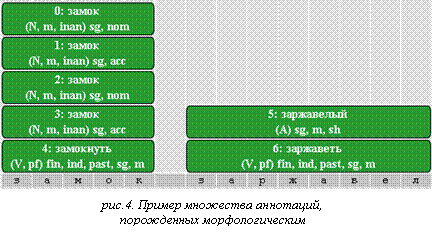Синтаксический анализатор осуществляет анализ множества аннотаций, порожденных морфологическим анализатором. В большинстве случаев это множество представляет собой упорядоченный набор "столбцов" из аннотаций, привязанных к словам текста (см. рисунок 4). Каждый "столбец" есть результат морфологического анализа соответствующего слова.

Анализатор работает с множеством синтаксических правил. Каждое правило из множества интерпретируется анализатором следующим образом: если в анализируемом множестве морфологических аннотаций встречаются тринотации, к которым применимо синтаксическое правило, то в ходе анализа эти тринотации могут быть связаны отношениями, указанными в правиле. Специально подчеркнем, что синтаксис правил не накладывает никаких ограничений на порядок тринотаций, сопоставляемых с шаблонами правил, и их контактность. В случае, когда ограничения такого рода лингвистически оправданы, их всегда можно указать в тексте правил в виде логических условий.

Анализатор читает морфологически аннотированный текст слева направо "столбец за столбцом", периодически откатываясь назад на то или иное количество слов и все время пытаясь построить оптимальную структуру, все элементы которой связаны синтаксическими правилами из множества правил. Для лучшего понимания переборного процесса приведем аналогию с шахматными алгоритмами. Аналог хода в шахматной партии – это применение одного из возможных на текущем шаге синтаксических правил. После того или иного хода ситуация на доске (текущая синтаксическая структура) меняется. Какие-то ходы (правила) становятся недопустимыми (неприменимыми), какие-то, наоборот, возможными (применимыми). Во всех современных шахматных алгоритмах используется понятие оценочной функции – функции, выражающей перспективность позиции на доске в некотором численном эквиваленте, что позволяет сравнивать между собой позиции. Это дает возможность заранее отсекать невыгодные варианты. Анализатор Treevial использует аналогичный аппарат для синтаксического анализа – аппарат лингвистически содержательных штрафных функций. Синтаксической структуре в системе сопоставляется n-мерный целый вектор, называемый штрафным вектором. Каждая компонента вектора отвечает за определенное свойство синтаксической структуры. Компонента №1, например, отвечает за степень непроективности структуры, а компонента №3 отражает количество зацеплений тринотаций. В ходе анализа для всех узлов дерева перебора определяется величина штрафного вектора. На каждом шаге перебора система выбирает для обработки узел, в котором норма штрафного вектора минимальна. Конструкции языка, позволяющего управлять штрафами описываются в разделе IV.

Перейдем к описанию языка синтаксических правил.

3. Синтаксические правила

Как уже говорилось, синтаксический анализатор работает со множеством синтаксических правил. Синтаксическое правило имеет следующую структуру:

rule <ruleName> {

<template1>,<template2>

::

<constraints>

=>

<action>

}

Понимать такое правило следует так: если два элемента входного множества тринотаций сопоставимы с шаблонами аннотаций <template1> и <template2>, удовлетворяют ограничениям <constraints> и над этими элементами может быть произведено действие <action> (набор элементарных преобразований над тринотациями и некоторые манипуляции с их атрибутами), то синтаксическое правило может быть применено анализатором на очередном шаге перебора. Опишем все структурные составляющие синтаксических правил, после чего более строго сформулируем условия применимости синтаксических правил.

Шаблон аннотации – это выражение, которое порождается следующей формальной грамматикой:

S à ‘(‘A’)’

A à S | A’,’A | E | A’|’A

E à <название атрибута>O<значение атрибута>

O à ‘=’ | ‘!=’

Шаблон аннотации следует понимать как логическое высказывание. Равенство или неравенство значения атрибута некоторой константе (нетерминал E) – это атомарные высказывания. Символ ‘,’ понимается как конъюнкция двух высказываний, а символ ‘|’ – как дизъюнкция. Для задания приоритета конъюнкций и дизъюнкций используются скобки.

Будем говорить, что тринотация удовлетворяет шаблону аннотации (сопоставима с шаблоном аннотации), если набор ее атрибутов не противоречит высказыванию, представленному шаблоном аннотации[1].

Шаблоны аннотаций используются для задания классов аннотаций, обладающих одинаковыми свойствами. Если аннотация – это точка некоторого пространства, то шаблон аннотации – это область в этом пространстве. Причем аннотация сопоставима с шаблоном тогда, когда соответствующая точка принадлежит соответствующей области.

Шаблоны аннотаций в синтаксических правилах могут именоваться. Имя шаблона пишется непосредственно перед шаблоном аннотации. Именование шаблонов используется для того, чтобы далее в тексте правила ссылаться на тринотации, сопоставляемые с шаблонами. Для ссылок такого рода используется специальный оператор ‘.’. Если требуется обратиться к атрибуту attr тринотации, сопоставленной с шаблоном Name, следует написать Name.attr. Приведем пример именованного шаблона аннотации. С этим шаблоном сопоставимы тринотации, соответствующие прилагательным и причастиям в единственном числе:

(1) C(NMB=sg,(POS=V,REPR=part | POS=A))

Блок <constraints> используется для того, чтобы накладывать на область применения правил ограничения, в которых участвуют атрибуты сразу нескольких тринотаций. Простым примером такого ограничения может служить согласование по падежу, т.е. равенство значений атрибута CAS (так в системе Treeton обозначается категория падежа) у нескольких тринотаций. Блок <constraints> представляет собой набор логических выражений над атрибутами тринотаций, сопоставляемых с шаблонами аннотаций. Логические выражения записываются через запятую. Для того, чтобы синтаксическое правило было применимо к двум тринотациям, необходимо обращение в истину всех его логических выражений при сопоставлении этих тринотаций с шаблонами. Далее приводится список конструкций, допустимых в логических выражениях блока <constraints>:

A != B – неравенство

A == B – равенство

A < , >, <=. >= B – операции сравнения

A && B – логическое «и»

A || B – логическое «или»

A ? B : C – условный переход. Если A, то B, иначе С.

A =p= B – штрафной оператор (см. раздел IV)

Приведем пример логического выражения, описывающего согласование по роду числу и падежу тринотаций, сопоставленных с шаблонами A и B:

(2) A.CAS == B.CAS && A.NMB == B.NMB && (A.NMB == pl ? true : A.GEND == B.GEND)

В блоке <action> описывается действие, которое совершает анализатор в случае применения синтаксического правила. Действие в данном случае – это набор последовательных элементарных преобразований текущей синтаксической структуры, в которых участвуют тринотации, сопоставленные с шаблонами аннотаций данного правила, и тринотации, создаваемые самим действием. Кроме того, в действие включается операция формирования наборов атрибутов создаваемых тринотаций. Для записи правил формирования этих наборов используются векторы присваивания.

Вектор присваивания – это заключенный в скобки набор элементарных присваиваний, записанных через запятую. Элементарные присваивания бывают трех типов:

1. Константное присваивание. Присваивание определенному атрибуту константного значения. Пример:

(3) CAS:=nom

2. Атрибутное присваивание. Присваивание определенному атрибуту значения атрибута тринотации, сопоставленной с определенным шаблоном аннотации. Пример:

(4) CAS:=A.CAS

3. Массовое присваивание. Копирование всего набора атрибутов из тринотации, сопоставленной с определенным шаблоном аннотации. Запись такого присваивания выглядит следующим образом:

(5) *:=A.*, где A – имя шаблона аннотации

Будем называть применением вектора присваивания к тринотации последовательное выполнение всех его элементарных присваиваний по отношению к этой тринотации. Приведем пример вектора присваивания:

(6) (*:=A.*,POS:=N,CAS:=B.CAS,NMB:=pl)

При применении этого вектора сначала наследуются все атрибуты тринотации, сопоставленной с A, затем в явном виде указывается часть речи (существительное), затем наследуется падеж тринотации, сопоставленной с B, после чего в явном виде указывается множественное число.

На данный момент в системе поддерживается 5 типов действий (шаблонам аннотаций A и B сопоставлены тринотации a и b соответственно):

1. Связывание

Запись: A -rel-> B

В результате этого действия выполняется преобразование link(a,b,rel).

2. Внедрение

Запись: A [B]

В результате этого действия выполняется преобразование addMemberStrong(a,b).

3. Унарная агрегация

Запись: (v)[A]

В результате этого действия сначала выполняется преобразование aggregateStrong(a), затем к созданной тринотации применяется вектор присваивания v.

4. Бинарная агрегация

Запись: (v)[A,B]

В результате этого действия сначала выполняется преобразование aggregateStrong(a). Обозначим созданную в результате тринотацию n. К тринотации n применяется вектор присваивания v. Затем выполняется преобразование addMemberStrong(n,b).

5. Агрегация со связыванием

Запись: (v)[A -rel-> B]

В результате этого действия сначала выполняется преобразование aggregateStrong(a). Обозначим созданную в результате тринотацию n. К тринотации n применяется вектор присваивания v. Затем выполняется преобразование link(a,b,rel).

В разделе I были описаны условия, при которых возможны элементарные преобразования тринотаций. Эти условия, в свою очередь, накладывают ограничения на область применения действий синтаксических правил. В общем случае не ко всякой паре тринотаций, сопоставленных с шаблонами правила и удовлетворяющих его ограничениям, можно применить элементарные преобразования, заложенные в действии синтаксического правила, т.к. эти преобразования могут нарушить аксиому 2 в определении тринотации. Если это все же возможно, то будем говорить, что действие синтаксического правила допустимо.

Следует также заметить, что синтаксический анализатор Treevial работает с тринотациями в режиме контроля за попарным непересечением тривиальных тринотаций. Это означает, что морфологические аннотации, из которых складываются синтаксические структуры, никогда не накладываются друг на друга.

Таким образом, синтаксическое правило может быть применено к двум тринотациям t₁ и t₂ тогда и только тогда, когда, во-первых, t₁ и t₂ сопоставимы с шаблонами аннотаций правила, во-вторых, при этом сопоставлении все логические выражения в блоке <constraints> истинны и, в-третьих, действие, указанное в правиле, допустимо при этом сопоставлении.

На рисунке 5 приводится набор правил, описывающий некоторые сочинительные конструкции в русском языке (рассматривается сочинение существительных).

Правило ConjNplSingle выделяет «элементарные конъюнкты», т.е. помещает в один новый агрегат некоторое существительное и союз «и», стоящий слева от него (B.start < C.start), при этом проводя между ними связь coord_conj. Созданная тринотация наследует часть атрибутов существительного и получает дополнительные атрибуты (AGGROTYPE:=ConjN, SINGLE:=single). Правило ConjNpl позволяет поместить в новую тринотацию два элементарных конъюнкта или единичное существительное и один элементарный конъюнкт. Легко видеть, что кроме ограничения на линейный порядок элементов, в этом правиле присутствует условие согласования конъюнктов по падежу (A.CAS == B.CAS). Результирующая тринотация наследует падеж конъюнктов и в явном виде получает характеристику множественного числа (NMB:=pl). Последнее правило (ConjEx) позволяет добавлять в уже созданный сочинительный агрегат конъюнкты в 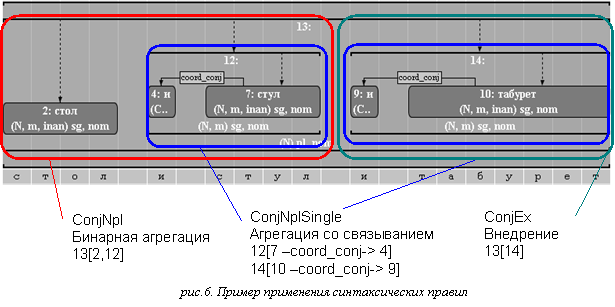том случае, если они согласуются с ним по падежу. Рисунок 6 иллюстрирует работу этих правил.

4. Штрафы

Алгоритм работы анализатора Treevial является переборным. В ходе анализа программа перебирает различные варианты применения синтаксических правил к аннотациям, порожденным морфологическим анализатором. При работе с предложениями большой длины количество перебираемых вариантов часто возрастает экспоненциально. Для борьбы с этой проблемой авторами был разработан аппарат лингвистически содержательных штрафных функций. Этот аппарат позволяет контролировать переборный процесс и направлять его в нужную сторону. Правила оценки синтаксических структур формулируются на специальном языке управления штрафами. Иными словами, язык управления штрафами позволяет задавать функцию для вычисления штрафного вектора по виду синтаксической структуры. В ходе анализа, используя указанную функцию на очередном шаге переборного процесса, система каждый раз выбирает для обработки узел дерева перебора, в котором норма штрафного вектора минимальна.

На сегодняшний день анализатором Treevial поддерживается 4 типа штрафов:

· штрафы на повторение

· штрафы на зацепление

· штрафы на расщепление

· штрафы на применение правил

Величина штрафного вектора P для синтаксической структуры вычисляется по следующей формуле:

P = P_r + P_h + P_s + P_u, где

P_r – величина вектора суммарного штрафа на повторение,

P_h – величина вектора суммарного штрафа на зацепление,

P_s – величина вектора суммарного штрафа на расщепление,

P_u – величина вектора суммарного штрафа на применение правил.

Размерность штрафного вектора определяется на подготовительном этапе, в момент считывания программой анализатора синтаксических правил. Эта размерность зависит от того, сколько компонент штрафного вектора используется штрафами на применение правил. Она всегда больше или равна 6, т.к. первые 6 компонент штрафного вектора зарезервированы для штрафов на повторение, зацепление и расщепление.

Правила вычисления вектора суммарного штрафа для каждого из типов штрафов приводятся ниже вместе с описанием самих типов.

Как уже говорилось, тривиальные узлы синтаксических структур, которые строит анализатор, не могут накладываться друг на друга. Благодаря этому на множестве тривиальных узлов синтаксической структуры можно ввести отношение линейного порядка <. Две аннотации связываются этим отношением, если начало первой из них в тексте расположено левее начала второй. Учитывая сказанное, можно заключить, что к множеству тривиальных узлов синтаксической структуры применим математический аппарат, изложенный в [Гладкий 1985: 13,14]. Нам понадобятся два понятия этого аппарата: понятие зацепления множеств и понятие расщепления множеств. Приведем определения этих понятий для тринотаций.

Пусть дана тринотация t, все тривиальные узлы дерева развертки которой попарно не пересекаются. Пусть P – множество тривиальных узлов дерева развертки тринотации t. Пусть E₁, E₂ ⊆ P, причем E₁ ∩ E₂ = ⌀.

Будем говорить, что E₁ и E₂ зацепляются, если существуют аннотации a,b ∈ E₁, c,d ∈ E₂, такие, что одна из аннотаций c,d лежит, а другая не лежит между a и b.

Будем говорить, что E₂ расщепляет E₁, если существуют аннотации a,b ∈ E₁, c ∈ E₂, такие, что c лежит между a и b.

Перейдем к описанию различных типов штрафов.

4.1 Штрафы на повторение

Штрафы на повторение используются в тех случаях, когда требуется ограничить количество связей одного типа, выходящих из одного узла синтаксической структуры. В качестве примера можно привести связь между глаголом и существительным в винительном падеже. В русском языке эта связь больше двух раз не повторяется (ср. “он играл эту симфонию всю ночь”).

Для задания штрафов на повторение используется набор штрафных правил, каждое из которых имеет следующий вид:

RepPenalties (rel) = {p₀,p₁,…,p_n},

где rel – тип синтаксической связи, p_i ≥ 0 (i: 0,1,2,…,n)

Такая конструкция задает функцию f_rel(d), сопоставляющую узлу d синтаксической структуры целое неотрицательное число:

f_rel(d) = p_k, если из d выходит k связей типа r и k ≤ n

f_rel(d) = p_n, если из d выходит больше чем n связей типа r

Суммарный штраф на повторение P_r представляет из себя вектор, в котором первая компонента равна ∑f_rel(d) (сумма берется по всем узлам синтаксической структуры и по всем штрафным правилам). Остальные компоненты вектора полагаются равными 0.

4.2 Штрафы на зацепление

Известно, что подавляющее большинство предложений естественного языка обладает свойством проективности. В связи с этим накладывание штрафов на непроективные варианты анализа становится очень мощным средством для уменьшения перебора. Более того, даже в том случае, когда правильный вариант анализа предложения непроективен, редко находится альтернативный неправильный (но формально допустимый) вариант анализа с меньшим уровнем непроективности. Поэтому непроективный вариант все равно оказывается первым в списке.

Поскольку тринотации, как уже говорилось, очень похожи на системы синтаксических групп, было решено оценивать степень непроективности тринотаций в соответствии с [Гладкий 1985, 50]. Три аксиомы А.В.Гладкого (аксиомa 3 из 1-ой группы и аксиомы 4,5 из 2-ой группы) легли в основу системы штрафов, которые мы назвали штрафами на зацепление.

Штрафы на зацепление делятся на RR-штрафы (аксиома 5), RT-штрафы (аксиома 4) и TT-штрафы (аксиома 3). R в приведенных аббревиатурах обозначает связь (relation), T обозначает тринотацию (treenotation). RR-штрафы ограничивают взаиморасположение связей, RT-штрафы ограничивают взаиморасположение связей и тринотаций, а TT-штрафы ограничивают взаиморасположение тринотаций.

RR-штрафы (см. рис.7)

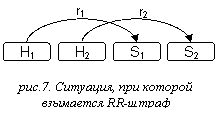Для накладывания RR-штрафов используется набор штрафных правил, каждое из которых имеет следующий вид:

HookingPenaltyRR (rel₁,rel₂) :: A,B,C,D = v,

где rel₁, rel₂ – типы связей, A, B, C, D – шаблоны аннотаций, v ≥ 0

Указанная конструкция задает функцию f_rel1,rel2(r₁,r₂), сопоставляющую двум неслужебным связям r₁,r₂ целое неотрицательное число.

Обозначим хозяина связи r₁ как h₁, а слугу как s₁. Хозяина связи r₂ обозначим как h₂, а слугу как s₂. Обозначим множества тривиальных узлов деревьев разверток тринотаций h₁, s₁, h₂, s₂ как H₁, S₁, H₂, S₂ соответственно.

f _rel1,rel2 (r₁,r₂) = v в том случае, когда r₁ имеет тип rel₁, r₂ имеет тип rel₂, множества H₁∪S₁ и H₂∪S₂ зацепляются и h₁, s₁, h₂, s₂ сопоставимы c A, B, C, D соответственно.

f _rel1,rel2 (r₁,r₂) = 0 в противном случае

Пусть в дереве развертки некоторой тринотации t есть k неслужебных связей r_i. Будем обозначать тип связи r_i как tp(r_i).

Определим матрицу H_RR(t) = {h_ij} (i=1,2,…,k;j=1,2,…,k) следующим образом:

h_ij = ∑f _{tp(ri), tp(rj)}(r_i,r_j), если i > j (сумма по всем RR-правилам указанного вида),

h_ij = 0 в остальных случаях

Матрица H_RR(t) понадобится нам для записи формулы вычисления суммарного штрафа на зацепление.

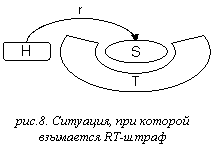RT-штрафы (см. рис.8)

Для накладывания RT-штрафов используются правила вида:

HookingPenaltyRT(rel) :: A,B,C = v,

где rel – тип связи, A, B, C – шаблоны аннотаций, v ≥ 0

Указанная конструкция задает функцию f_rel(t,r), сопоставляющую неслужебной связи r и тринотации t целое неотрицательное число.

Обозначим хозяина связи r как h, а слугу как s. Обозначим множества тривиальных узлов деревьев разверток тринотаций h, s, t как H, S и T соответственно.

f_rel(t,r) = v в том случае, когда r имеет тип rel, множества H∪ S и T зацепляются и h, s, t сопоставимы c A, B и C соответственно.

f_rel(t,r) = 0 в противном случае.

Пусть в дереве развертки некоторой тринотации t есть k тринотаций t_i и l неслужебных связей r_j. Определим матрицу H_RT(t) = {h_ij} (i=1,2,…,k;j=1,2,…,l) следующим образом:

h_ij = ∑f_rel (t_i,r_j) (сумма по всем RT-правилам)

Матрица H_RT(t) понадобится нам для записи формулы вычисления суммарного штрафа на зацепление.

TT-штрафы (см. рис.9)

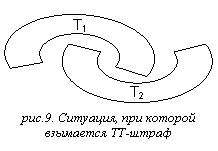Для накладывания TT-штрафов используются правила вида:

HookingPenaltyGG :: A,B = v,

где A, B – шаблоны аннотаций, v ≥ 0

Указанная конструкция задает функцию f(t₁,t₂), сопоставляющую тринотациям t₁ и t₂ целое неотрицательное число.

Обозначим множества тривиальных узлов деревьев разверток тринотаций t₁ и t₂ как T₁ и T₂ соответственно.

f(t₁,t₂) = v в том случае, когда множества T₁ и T₂ зацепляются и t₁, t₂ сопоставимы c A и B соответственно.

f(t₁,t₂) = 0 в противном случае.

Пусть в дереве развертки некоторой тринотации t есть k тринотаций t_i. Определим матрицу H_TT(t) = {h_ij} (i=1,2,…,k;j=1,2,…,k) следующим образом:

h_ij = ∑f (t_i,t_j), если i > j (сумма по всем TT-правилам)

h_ij = 0 в противном случае

Cуммарный штраф на зацепление P_h для некоторой синтаксической структуры t определяется следующим образом:

P_h = (0, ∥H_RR(t)∥,∥H_RT(t)∥,∥H_TT(t)∥,0,...,0), где ∥M∥ – эвклидова норма матрицы M.

4.3 Штрафы на расщепление

По аналогии с предыдущим пунктом вводятся штрафы на расщепление. Эти штрафы ограничивают количество обрамлений, допустимых в синтаксических структурах. Прототипом для них стали аксиомы, отличающие сильные системы синтаксических групп (СССГ) [Гладкий 1985: 54](аксиомы 6,7) от обычных ССГ. В соответствии с аксиомами штрафы на расщепление бывают двух типов: SR-штрафы и SRR-штрафы (S – англ. “split”, R – как и прежде, “relation”).

SR-штрафы (см. рис.10)

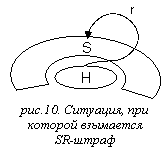Для накладывания SR-штрафов используются правила вида:

SplittingPenaltyR (rel) :: A,B = v,

где rel – тип связи, A, B – шаблоны аннотаций, v ≥ 0

Указанная конструкция задает функцию f_rel(r), сопоставляющую неслужебной связи r целое неотрицательное число:

Обозначим хозяина связи r как h, а слугу как s. Обозначим множества тривиальных узлов деревьев разверток тринотаций h, s как H, S соответственно.

f_rel(t,r) = v в том случае, когда r имеет тип rel, H расщепляет S и h, s сопоставимы c A и B соответственно.

f_rel(t,r) = 0 в противном случае.

Пусть в дереве развертки некоторой тринотации t есть k неслужебных связей r_j. Обозначим S_R(t) вектор вида (s₀,s₁,…,s_k), в котором s_i = ∑f_rel (r_j) (сумма по всем НR-правилам). Этот вектор понадобится нам для вычисления суммарного штрафа на расщепление.

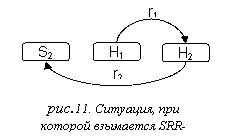SRR-штрафы (см. рис.10)

Для накладывания SRR-штрафов используются правила вида:

SplittingPenaltyRR (rel₁,rel₂) :: A,B,C = v,

где rel₁, rel₂ – типы связей, A, B, C – шаблоны аннотаций, v ≥ 0

Указанная конструкция задает функцию f_rel1,rel2(r₁,r₂), сопоставляющую двум неслужебным связям r₁,r₂ целое неотрицательное число:

Обозначим хозяина связи r₁ как h₁, а слугу как s₁. Хозяина связи r₂ обозначим как h₂, а слугу как s₂. Обозначим множества тривиальных узлов деревьев разверток тринотаций h₁, h₂, s₂ как H₁, H₂, S₂ соответственно.

f _rel1,rel2 (r₁,r₂) = v в том случае, когда r₁ имеет тип rel₁, r₂ имеет тип rel₂, кроме того s₁ совпадает с h₂, H₁ расщепляет H₂∪S₂ и h₁, h₂, s₂ сопоставимы c A, B, C соответственно.

f _rel1,rel2 (r₁,r₂) = 0 в противном случае.

Пусть в дереве развертки некоторой тринотации t есть k неслужебных связей r_i. Будем обозначать тип связи r_i как tp(r_i).

Определим матрицу S_RR(t) = {s_ij} (i=1,2,…,k;j=1,2,…,k) следующим образом:

s_ij = ∑f _{tp(ri), tp(rj)}(r_i,r_j), если i > j (сумма по всем SRR-правилам, указанного вида),

s_ij = 0 в остальных случаях

Cуммарный штраф на зацепление P_s для некоторой синтаксической структуры t определяется следующим образом:

P_s = (0, 0, 0, 0, ∥S_R(t)∥,∥S_RR(t)∥, 0,...,0)

4.4 Штрафы на применение правил

Штрафы на применение правил используются в тех случаях, когда требуется наложить штраф на то или иное явление, сопряженное с применением некоторого синтаксического правила. Примером может служить штраф на обратный порядок существительного и прилагательного при образовании атрибутивной связи между ними («человек умный» вместо «умный человек»). Штрафы на правила указываются в тексте синтаксических правил внутри блока ограничений. В логических выражениях этого блока может использоваться специальная конструкция вида:

(p₀,p₁,…,p_n) =p= C, где p_i ≥ 0, С – логическое выражение

Понимать такую конструкцию следует так: если при проверке ограничений некоторого синтаксического правила R выполняется оператор =p= и выражение С при этом обращается в истину, то система соотносит с правилом R штрафной вектор вида (0,0,0,0,0,0,p₀,p₁,…,p_n,0,...,0). При подсчете суммарного штрафа на правила некоторой синтаксической структуры t, система просто суммирует все штрафные вектора, соотнесенные с правилами, участвовавшими в образовании синтаксической структуры. На рисунке 12 приводится пример правила, позволяющего связывать согласованные прилагательные и существительные. В случае, когда существительное стоит перед прилагательным, взымается штраф равный 5.

5. Заключение

В данный момент авторы работают, в первую очередь, над формированием свода синтаксических правил русского языка для анализатора Treevial. Особое внимание уделяется балансировке штрафов. Параллельно ведется работа по развитию аппарата тринотаций, в частности, той части этого аппарата, которая связана с шаблонами тринотаций. Кроме того, авторами ведутся исследования, связанные с обработкой эллиптических конструкций.

В заключение следует сказать, что вся описанная работа вряд ли могла бы быть проделана без помощи трех коллег: авторы горячо признательны С.А.Старостину за предоставленные разработки в области русской морфологии и серию продолжительных бесед о русском синтаксисе. Мы благодарим Н.В.Перцова за его неоценимые консультации, а также С.А.Минора за ряд ценных замечаний и практическую помощь.

Список литературы

1. Гладкий 1985 – А.В.Гладкий. Синтаксические структуры естественного языка в автоматизированных системах общения. – М.: Наука, 1985.

2. Мальковский 1985 – Мальковский М.Г. Диалог с системой искуственного интеллекта. – М.: изд-во МГУ, 1985.

3. Перцов, Старостин 1999 – Н.В. Перцов, С.А. Старостин. О синтаксическом процессоре, работающем на ограниченном объеме лингвистических средств // Труды международной конференции Диалог'1999, т.2. – Таруса: 1999. С. 224-230.

4. Cunningham a.o. 2002 – H.Cunningham, D.Maynard, K. Bontcheva, V.Tablan. GATE: an Architecture for Development of Robust HLT Applications // Proceedings of the 40th Annual Meeting of the Association for Computational Linguistics (ACL), Philadelphia, July 2002.

5. Shafirin a.o. 2004 – V.Karasev, V.Khoroshevsky, A.Shafirin. New Flexible KRL JAPE+: Development & Implementation // Knowledge-Based Software Engineering. Proceedings of the Sixth Joint Conference on Knowledge-Based Software Engineering // Amsterdam etc., 2004.

---

[1] Читателя может смутить, что тринотации сопоставляются с шаблонами аннотаций, а не тринотаций. Дело в том, что термин шаблон тринотации имеет свое собственное значение. Шаблоном тринотации следует называть некую формальную запись, накладывающую ограничения как на атрибуты тринотации, так и на ее внутреннюю структуру. Формальный аппарат шаблонов тринотаций в данный момент разрабатывается авторами. Описание этого аппарата выходит за рамки данной статьи.